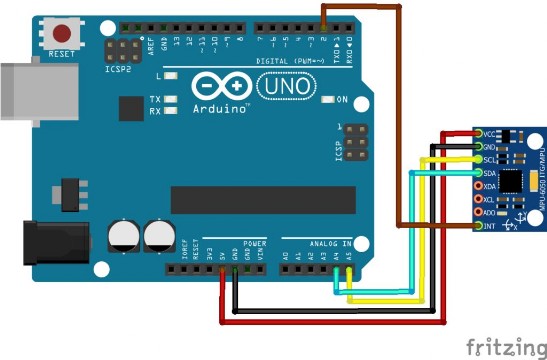
Módulo Acelerómetro y giroscopio
Arduino > shelds
El Módulo MPU-6050 es una IMU de 6DOF (se lee “6 Degrees Of Freedom“). Esto significa que lleva un acelerómetro y un giroscopio, ambos de 3 ejes (3+3 = 6DOF).

Antes de empezar, ¿qué es una IMU ? Se trata de un dispositivo capaz de mesurar la fuerza (acceleración) y la velocidad. Genéricamente consta de un Acelerómetro y un Giroscopio. Por lo tanto: una IMU no mesura ángulos . Por lo menos no directamente, requiere algunos cálculos.
El MPU-6050 opera con 3.3 voltios, por eso llevan un regulador que permite conectarla a 5V.
utiliza el protocolo de comunicación I2C.

Documentación:
Tutorial de uso
Producto totalmente compatible.